ode45(g,[0,20],[1;0])
(Continuation of Using Matlab for First Order ODEs)
Example problem: The angle y of a driven pendulum satisfies the differential equation
y'' = -sin(y) + sin(5 t)
and the initial conditions
y(0) = 1
y'(0) = 0.
If your problem is of order 2 or higher: rewrite your problem as a first order system. Let y1=y and y2=y', this gives the first order system
y1' = y2,
y2' = -sin(y1) + sin(5 t)
with the initial conditions
y1(0) = 1
y2(0) = 0.
Define an inline function g for the
right hand side of the first order system: Note that g
must be specified as a column vector using
[...;...] (not a row vector
using [...,...]). In the definition of g,
use y(1) for y1, use
y(2) for y2. The definition of
g should have the form
g = inline('[expression for y1';expression for y2']', 't', 'y');
You have to use inline(...,'t','y'), even if t does
not occur in your formula. For our example the first component of g
is y2, the second component is -sin(y1)
+ sin(5 t) and we define
g = inline('[ y(2); -sin(y(1))+sin(5*t) ]', 't', 'y')
To plot the numerical solution: To obtain
plots of all the components of the solution for t going from t0 to t1 use
ode45(g,[t0,t1],[y10;y20]) where y10,
y20 are the initial values for y1,
y2 at the starting point t0. In our example we
get a plot for t going from 0 to 20 with the initial values
[1;0] using
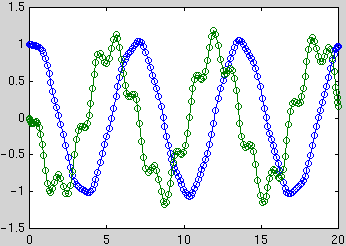
ode45(g,[0,20],[1;0])
This shows the two functions y1(t)=y(t) (blue) and y2(t)=y'(t) (green).
The circles mark the values which were actually computed (the points are
chosen by Matlab to optimize accuracy and efficiency). You can obtain a vector
ts and a matrix ys with the coordinates of these
points using [ts,ys] = ode45(g,[t0,t1],[y10;y20]).
You can then plot the solution curves using
plot(ts,ys) (this is a way to obtain a plot
without the circles). Note that each row of the matrix ys contains
2 entries corresponding to the two components of the solution at that time:
[ts,ys] = ode45(g,[0,20],[1;0]); % find ts, ys, but don't show
plot(ts,ys) % make plot of y1 and y2 vs. t
[ts,ys] % show table with 3 columns for t, y1, y2
You can obtain the vector of y1 values in the first column of
ys by using ys(:,1), therefore
plot(ts,ys(:,1)) plots only y1(t).
To obtain numerical values at specific
t values: You can
specify a vector tv of t values and use [ts,ys] =
ode45(g,tv,[y10;y20]). The first element of the vector
tv is the initial t value; the vector tv must have at
least 3 elements. E.g., to obtain the solution with the initial values
[1;0] at t = 0, 0.5, ..., 10 and display the results as a table
with 3 columns t, y1, y2,
use
[ts,ys]=ode45(g,0:0.5:10,[1;0]);
[ts,ys]
To plot trajectories in the phase plane: To see the points with coordinates ( y1(t), y2(t) ) in the y1, y2 plane for t going from 0 to 20 type
options=odeset('OutputFcn','odephas2');
ode45(g,[0,20],[1;0],options)
This shows the points while they are being computed (the plotting can be stopped with the stop button). To first compute the numerical values and then plot the curve without the circles, type
[ts,ys] = ode45(g,[0,20],[1;0]); % find ts, ys, but don't show
plot(ys(:,1),ys(:,2)) % make plot of y2 vs. y1
If the right hand side function g(t, y) does not depend on t, the problem is called autonomous. In this case the behavior of the differential equation can be visualized by plotting the vector g(t, y) at each point y = (y1,y2) in the y1,y2 plane (the so-called phase plane).
First save the files vectfield.m
and vectfieldn.m
into your home directory.
To plot the vector field for y1 going from
a1 to b1 with a spacing of d1 and y2 going from a2 to b2 with a spacing of d2
use vectfield(g,a1:d1:b1,a2:d2:b2). The command
vectfieldn works in the same way, but produces
arrows which all have the same length. This makes it easier to see the direction
of the vector field.
Example: The pendulum problem without the driving force has the differential equation y'' = -sin(y). This gives the first order system
y1' = y2,
y2' = -sin(y1)
Here we define
g = inline('[y(2);-sin(y(1))]','t','y')
We can plot the vector field and 10 trajectories with starting points (0,0), (0,0.3), ..., (0,2.7) in the phase plane as follows:
vectfield(g,-2:.5:8,-2.5:.25:2.5) hold on for y20=0:0.3:2.7 [ts,ys] = ode45(g,[0,10],[0;y20]); plot(ys(:,1),ys(:,2)) end hold off
Use the dsolve command. Specify all
differential equations as strings, using
Dy for y'(t),
D2y for y''(t) etc. .
For an initial value problem specify the initial conditions
in the form 'y(t0)=y0',
'Dy(t0)=y1' etc. . The last argument of
dsolve is the name of the independent variable, e.g.,
't'.
Example: For the differential equation
y'' = -y + sin(5 t)
use
sol = dsolve('D2y = -y + sin(5*t)','t')
In this case, the answer can be simplified by typing
s = simple(sol)
which gives the general solution
-1/24*sin(5*t)+C1*cos(t)+C2*sin(t) with two constants
C1, C2.
To solve the ODE with initial conditions y(0) = 1, y'(0) = 0 use
sol = dsolve('D2y = -y + sin(5*t)','y(0)=1','Dy(0)=0','t')
Then s = simple(sol) gives the solution
-1/24*sin(5*t)+5/24*sin(t)+cos(t).
To plot the solution curve use
ezplot:
ezplot(sol, [0,20])
To obtain numerical values at one or more t values proceed exactly as in the case of a first order ODE.
Example for system of ODEs: For the system
y1' = y2,
y2' = -y1 + sin(5 t)
with the initial conditions
y1(0) = 1
y2(0) = 0
type
sol = dsolve('Dy1=y2','Dy2=-y1+sin(5*t)','y1(0)=1','y2(0)=0','t')
which gives the somewhat strange response
sol =
y1: [1x1 sym]
y2: [1x1 sym]
This means that the two components of the solution can be accessed as
sol.y1 and sol.y2 :
Typing
sol.y1
gives
-2/3*sin(t)*cos(t)^4+1/2*sin(t)*cos(t)^2+1/6*sin(t)+cos(t). This
can be simplified by typing
s1 = simple(sol.y1)
which gives -1/24*sin(5*t)+5/24*sin(t)+cos(t). For the second
component y2 of the solution we proceed in the same way: Typing
s2 = simple(sol.y2)
gives -sin(t)-5/24*cos(5*t)+5/24*cos(t).
To plot the solution curves use
ezplot:
ezplot(sol.y1, [0,20])
hold on
ezplot(sol.y2, [0,20])
hold off
To obtain numerical values use
double(subs(sol.y1,'t',tval)) where tval is a number
or a vector of numbers. E.g., the following commands generate a table with three
columns t, y1, y2 for t=0, 0.5, ...,
10:
tval = (0:0.5:10)'; % column vector with t-values
yval = double(subs([sol.y1,sol.y2],'t',tval)); % 2 columns with y1,y2
[tval, yval] % display 3 columns together
To plot the solution in the phase plane use a similar approach with more t values:
tval = (0:0.1:10)'; % column vector with t-values
yval = double(subs([sol.y1,sol.y2],'t',tval)); % 2 columns with y1,y2
plot(yval(:,1),yval(:,2)) % plot col.2 of yval vs. col.1 of yval
 tvp@math.umd.edu
tvp@math.umd.edu